Chapter 2 Statistical modelling
Was Paul truly psychic, an oracle of some kind? Or was Paul – or his keeper, as what does fame really mean to an octopus? – just really lucky? How do we know? And what really are the chances of predicting the winner of 8 matches correct? These are questions we will focus on now.
In this chapter, we will start defining statistical models and using them to make inferences about the Data Generating Process. We will cover some basic probability theory, and use this to define two alternative models of Paul’s predictions. One in which he is randomly guessing, and one in which his predictions can be more (or less) accurate than if he were randomly guessing, while we are unsure about how accurate Paul really is in that case. We will discuss how to estimate the unknown accuracy of Paul’s predictions in this model. After this, we will try to answer the question: was Paul (somewhat) psychic? Our answer will be based on whether we can refute the hypothesis that he was randomly guessing. This is generally done with a procedure called a null-hypothesis significance test.
2.1 Coin flipping: Defining a statistical model
What does it mean for Paul to be psychic, to be an oracle? Sometimes it is easier to answer this question by considering the opposite: When would Paul not be an oracle? If Paul had no way to tell the future, he would be “merely guessing”. Purely random guessing between two options can be implemented by flipping a coin. Suppose Paul made his choices by “flipping a mental coin”, and choosing the box on the left when the outcome was “heads”, and the box on the right when the outcome was “tails”. Great, we now have a model of the Data Generating Process! Coin flipping can be seen as a physical model. It is something that we can do in the real world, as many times as we want. Because we understand the physical properties of coin flips reasonably well – it is really difficult to predict the outcome of a coin flip – it works well as a model of random guessing. But flipping coins over and over is rather tedious. If we have a mathematical description, a statistical model, of flipping coins, we can spare ourselves this trouble. To do so, we first need to know a bit more about probability.
2.2 Probability
Let’s simulate Paul’s decisions for the 2010 FIFA World cup. Grab a coin and flip it 8 times. What are the outcomes? When I did this, the outcomes were:
tails, tails, tails, heads, tails, heads, heads, tails
Remember, Paul would go left upon heads, and right upon tails. Following these rules, Paul’s decisions are then:
right, right, right, left, right, left, left, right
To know whether these guesses are correct or incorrect, we need to know which team was placed in which box. This information is provided in Table 1.2: the first country under Match is the box on the left, and the second the box on the right. Using this, our simulation then provides the following:
incorrect, correct, correct, correct, correct, correct, incorrect, correct
So in our simulation, Paul made 6 correct predictions out of 8. Not quite as good as the real Paul, but still a reasonable performance.
Notice how we went through quite a few steps. We defined a model of non-psychic-and-guessing Paul as making decisions by flipping a coin, we then simulated Paul’s decisions by flipping a coin, then transformed these coin flips into a variable containing the decisions to open the left or right box, and finally transformed this variable into another variable containing the accuracy of the predictions. The first transformation is easy. We could have simply put stickers on the coin relabelling “heads” as “left” and “tails” as “right”. The second transformation is not as obvious as it depends on a second variable (whether the winning team was represented by the left or right box). In this case, we could have saved ourselves a bit of work by immediately relabelling our coin flips as “correct” or “incorrect”. To see why, we need to know a bit more about how to calculate probabilities.
Let’s start at the beginning. For one coin flip, there are two possible outcomes: the coin lands on heads or on tails. The outcome can’t be neither (we are assuming the coin is thin enough to not land on its side), nor two heads, or something else. The coin must land on either heads or tails, so there are two outcomes. We call the set of all possible outcomes the outcome space, and we’ll use a nice curly \(\mathcal{S}\) to denote it:
\[\mathcal{S} = \{\text{heads},\text{tails}\}\]
Our coin flip is a random variable that takes one of the values in the outcome space. It is traditional to denote random variables with capital Roman letters, and the values with small Roman letters. When we want to make generic statements that apply to different random variables (such as a coin flip, the roll of a die, the outcome of a prediction), we tend to use this notation, and \(p(Y=y)\) then means ‘The probability that random variable \(Y\) has value \(y\)’. Other times, it may be easier to use more descriptive names. In this book, when we use a name for a variable, we will use a computer font, such as coin_flip, for the random variable. So \(p(\texttt{coin_flip} = \text{heads})\) means ‘The probability that random variable coin_flip has the value “heads”’.
2.2.1 What is probability?
I have just introduced the word “probability” without telling you what it means. You probably have some intuition yourself, for instance that probability is the chance of something happening. You might be surprised to know that even though statisticians can all perform probability calculations comfortably, there is quite some disagreement on what probability means. According to the traditional, Frequentist view, probability means long-run relative frequency. For instance, the probability of a coin flip landing on heads is defined as the proportion of times a coin lands heads when I flip a coin for a very, very large number of times. Table 2.1 shows the outcome and relative frequency calculations for 15 coin flips.
| flip | outcome | cumulative frequency heads | relative frequency heads |
|---|---|---|---|
| 1 | tails | 0 | 0.000 |
| 2 | tails | 0 | 0.000 |
| 3 | heads | 1 | 0.333 |
| 4 | heads | 2 | 0.500 |
| 5 | heads | 3 | 0.600 |
| 6 | tails | 3 | 0.500 |
| 7 | tails | 3 | 0.429 |
| 8 | tails | 3 | 0.375 |
| 9 | tails | 3 | 0.333 |
| 10 | tails | 3 | 0.300 |
| 11 | tails | 3 | 0.273 |
| 12 | tails | 3 | 0.250 |
| 13 | heads | 4 | 0.308 |
| 14 | heads | 5 | 0.357 |
| 15 | heads | 6 | 0.400 |
Figure 2.1 shows the relative frequency (i.e. the proportion) of heads after each coin flip, when flipping a coin for 2000 times. As you can see, the relative frequency fluctuates quite a bit, but becomes more stable with more flips. But even after 2000 flips, it is not equal to 0.5.
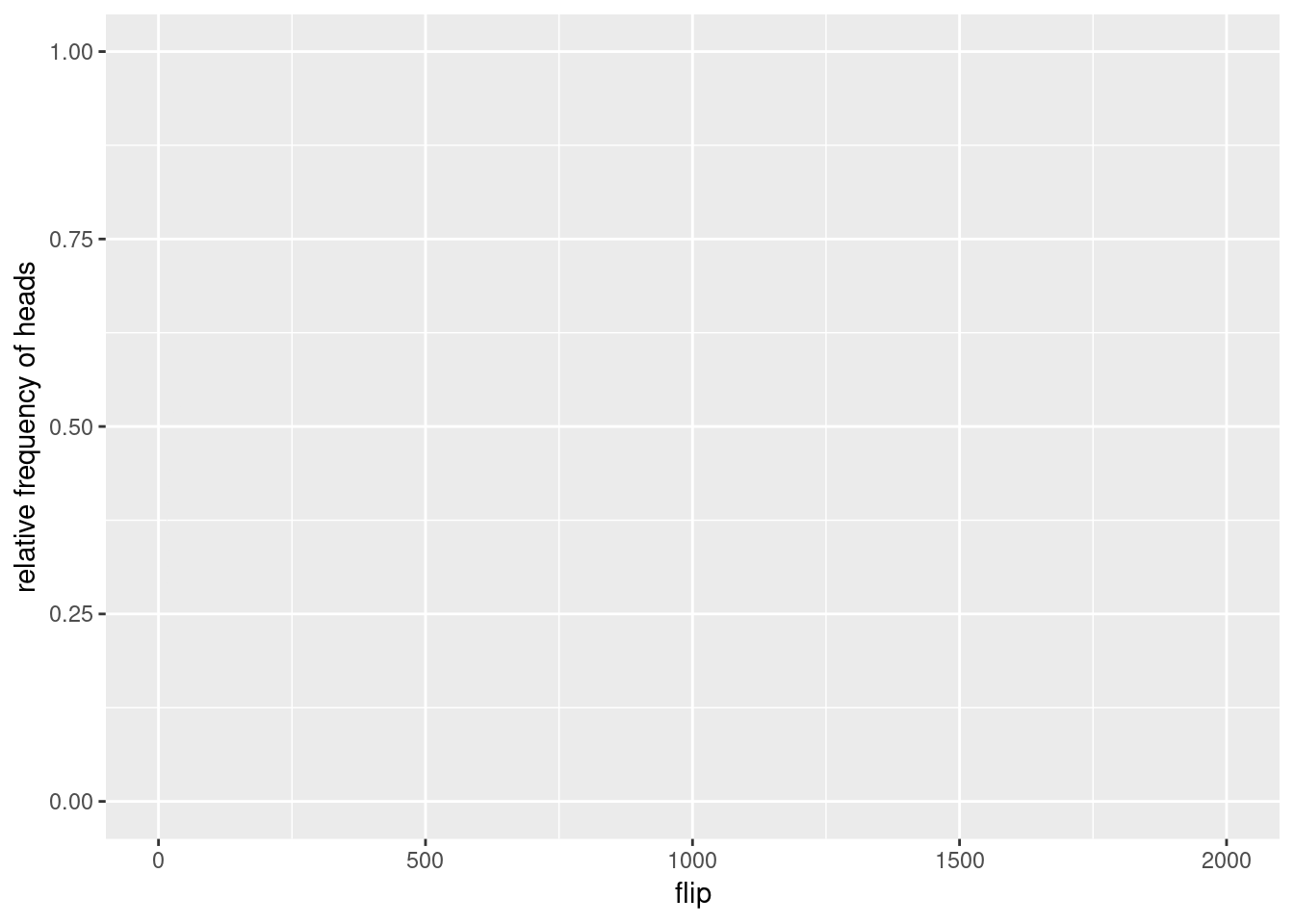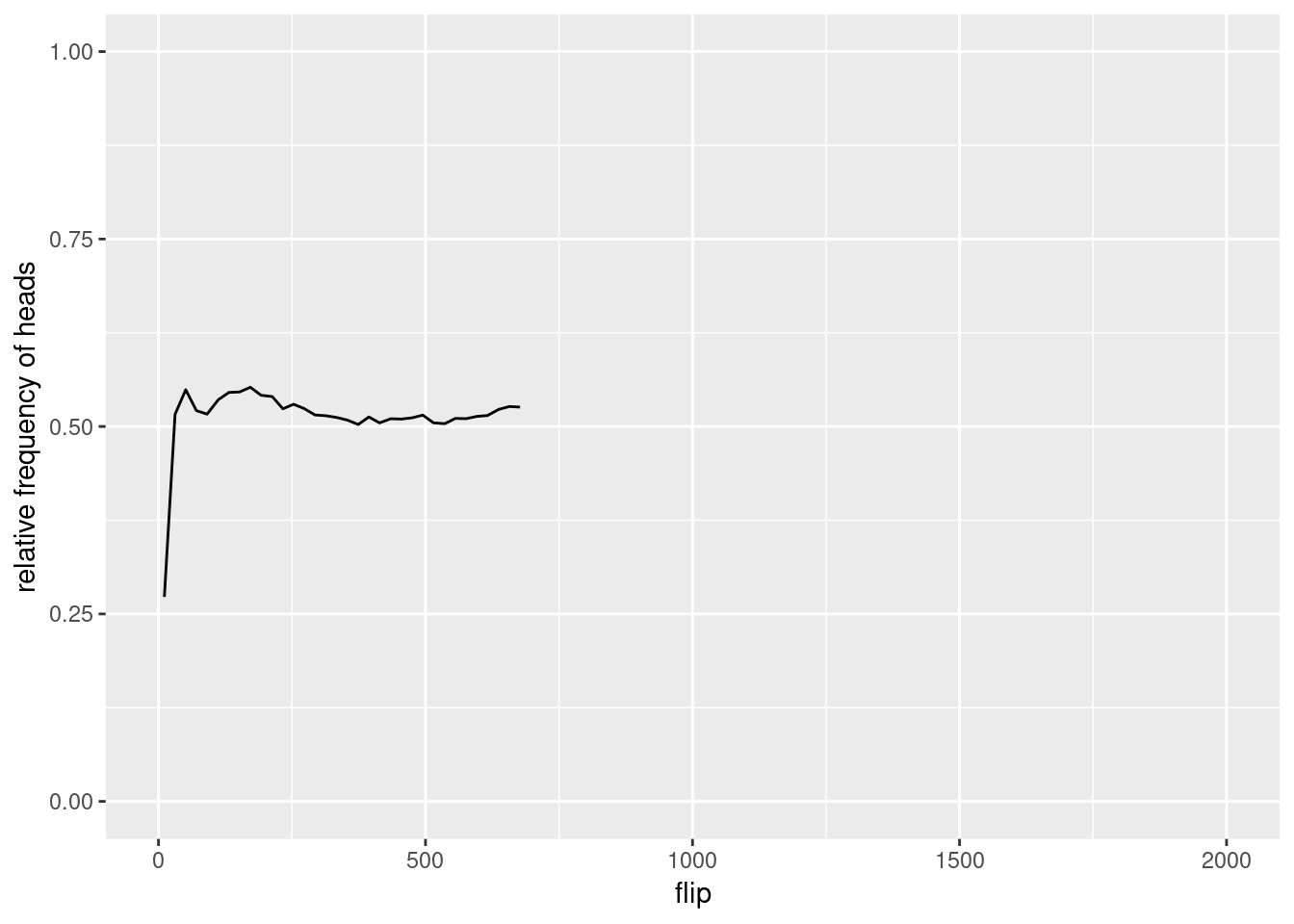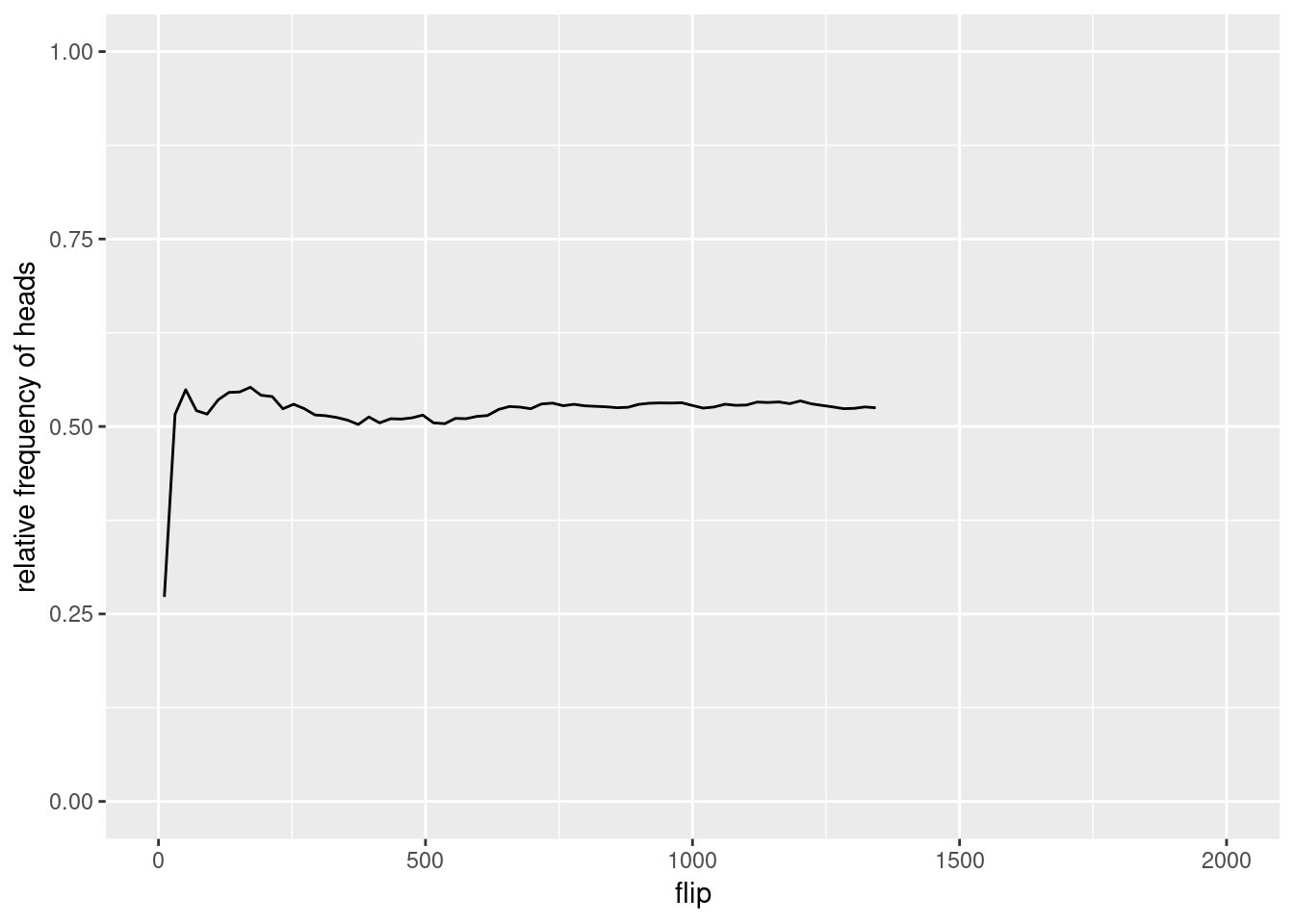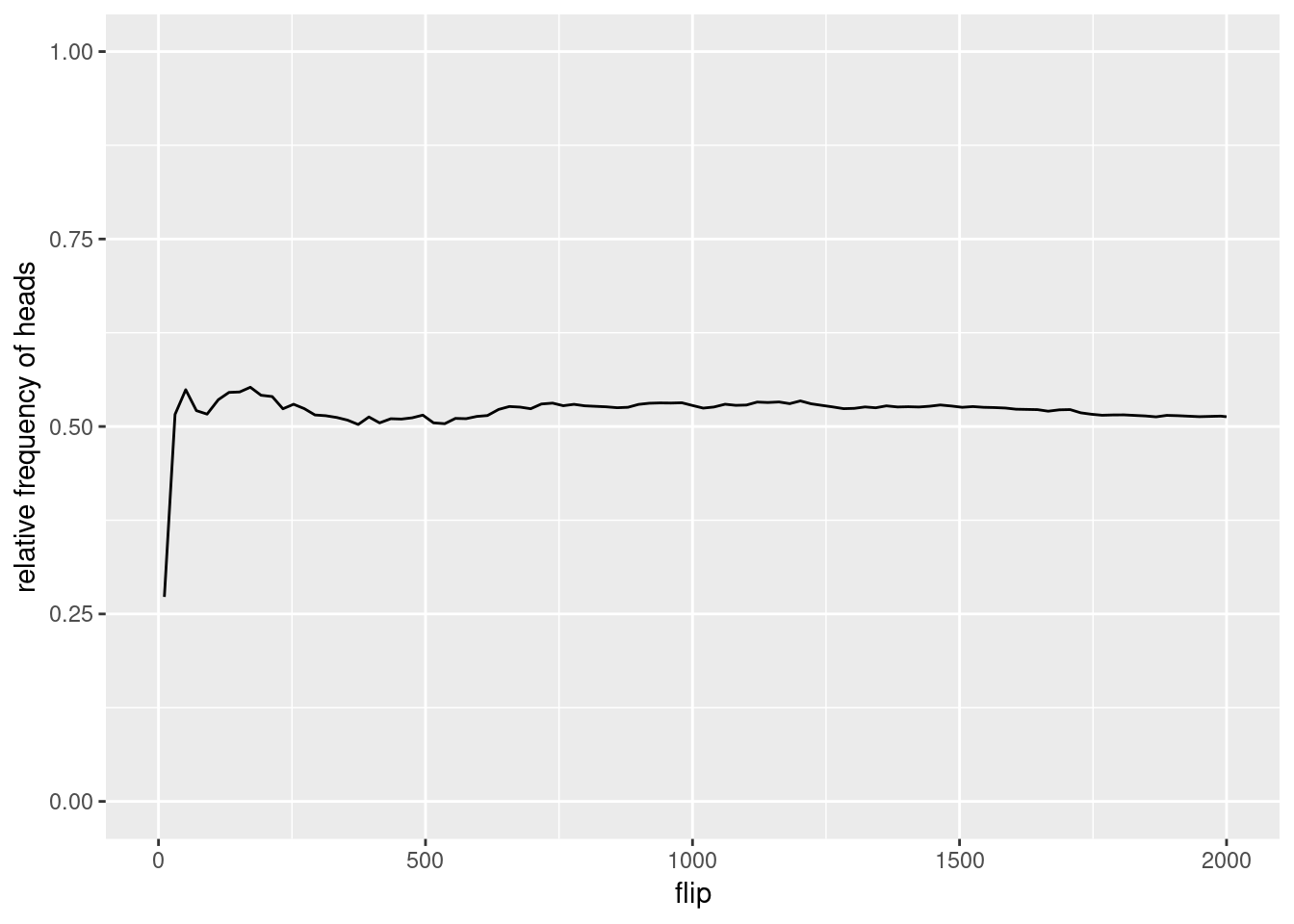
Figure 2.1: Relative frequency of heads when flipping a coin for 2000 times
Flipping a coin can be viewed as an experiment, that we can repeat. Figure 2.2 shows the results of flipping a coin for 5000 times when repeating the experiment 5 times. As you can see, the results of our experiments (the relative frequencies) are different each time. The differences are quite marked for a small number of flips, but become more alike after flipping the coin more times. This illustrates something known as The Law of Large Numbers, to which we will come back soon. For now, let’s focus on a different matter. If probability is a relative frequency, then which one is it? Each repetition of the experiment, as well as each number of throws, would give us a different answer!
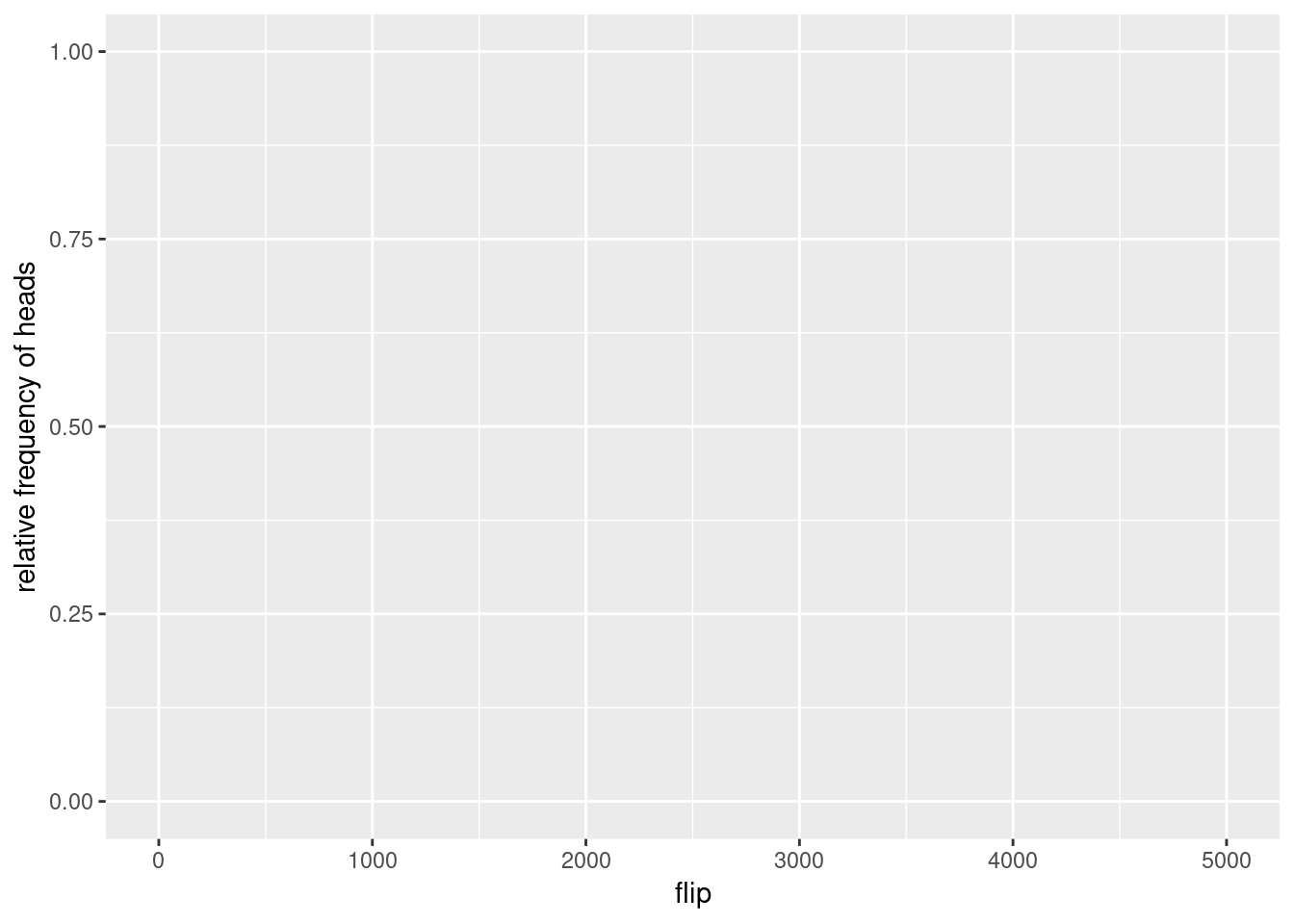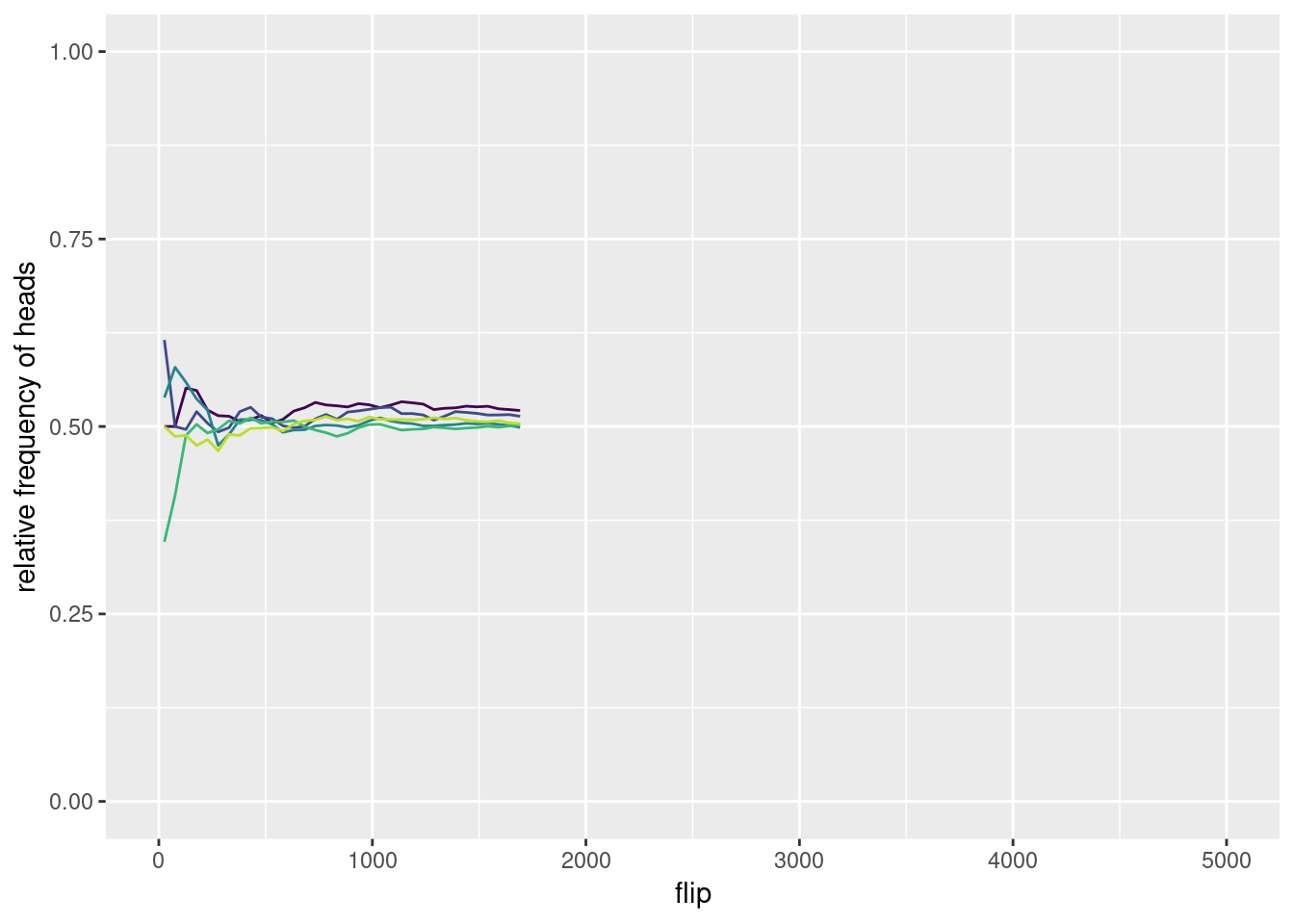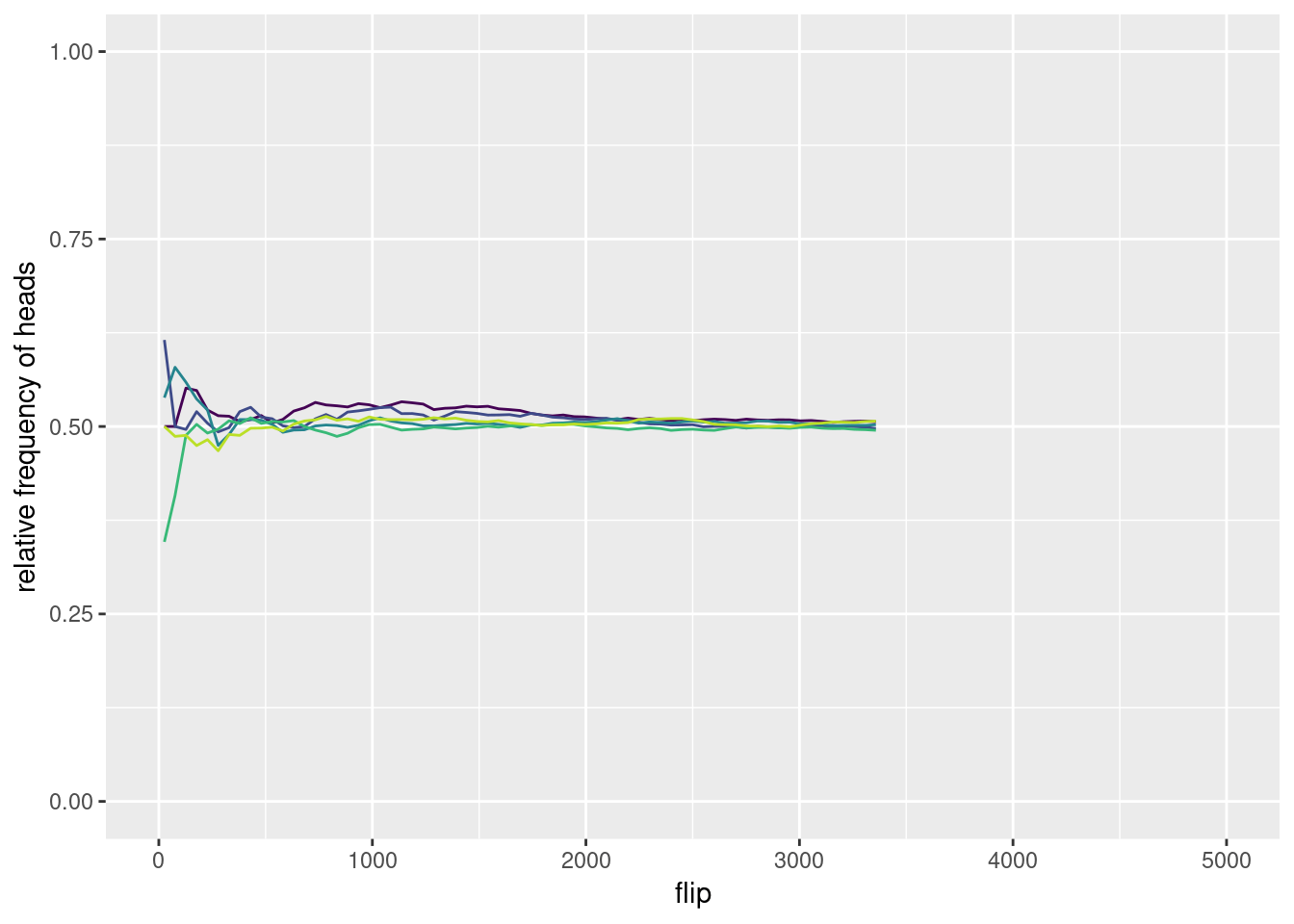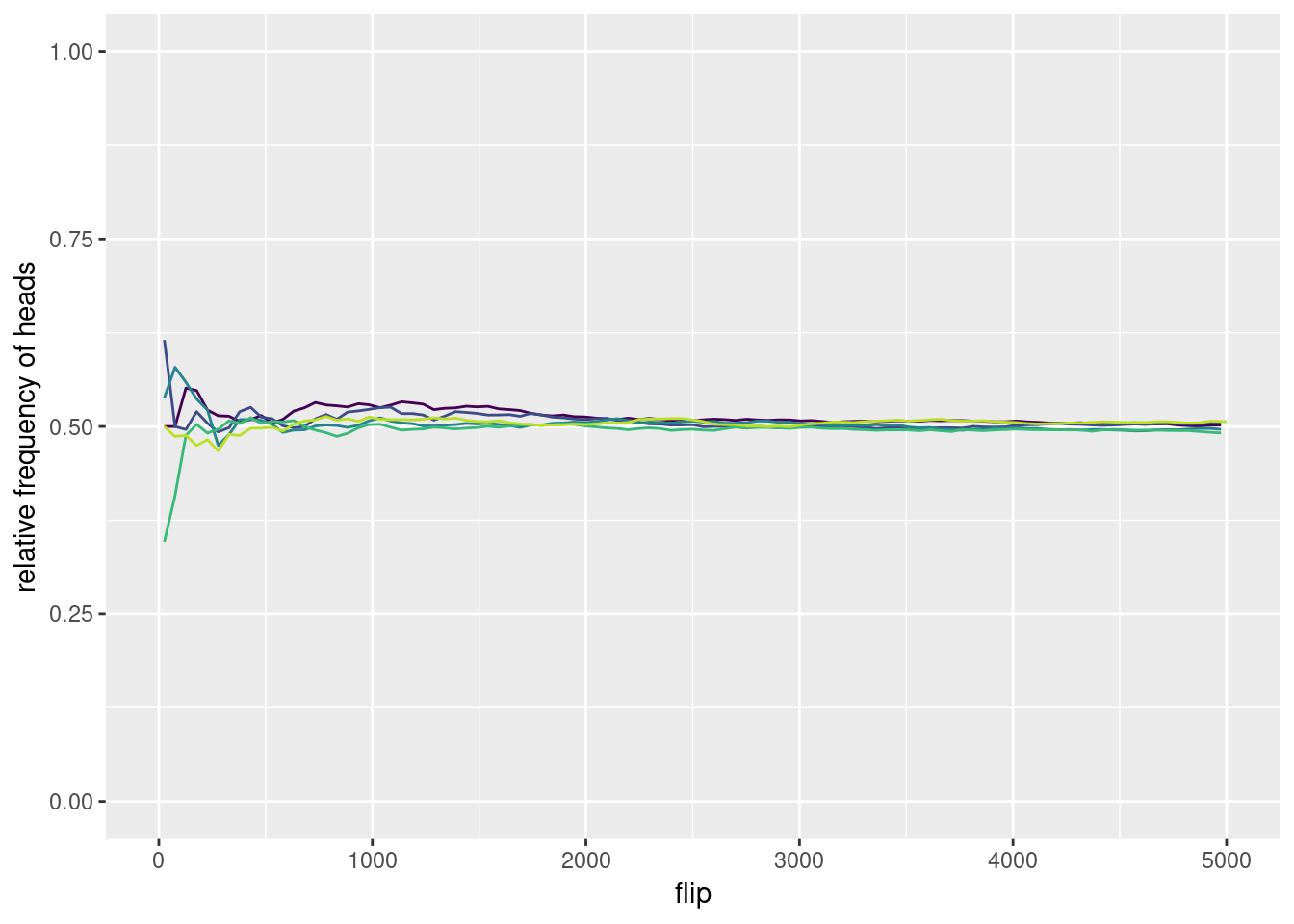
Figure 2.2: Relative frequency of heads when flipping a coin 5 times for 5000 times
To give a single answer, a “long-run relative frequency” must be the relative frequency when flipping the coin for an infinite number of times. That may seem disappointing. A nice aspect of the Frequentist View is that probabilities are something of the real world, but surely, we can’t flip a coin for an infinite number of times in the real world. That is true, but to understand what probability is, we don’t necessarily have to perform such infinite experiments. When we have to estimate the probability from a given (non-infinite) number of coin flips, we do have to worry about these issues. This, indeed, is what statistics is about: dealing with sample variability to estimate and infer unknown things. But for defining what a probability is, we can use mathematics to show that the long run relative frequency converges to a single number as the number of coin flips gets closer and closer to infinity. Which, in other words, means there is a single long-run relative frequency, and hence the probability is mathematically well-defined.
There is an alternative to the Frequentist View, called the Bayesian view or Subjective view, according to which probability means a rational degree of belief. This, in a sense, takes probability out of the real world, and into our minds. By doing so, it allows statements of probabilities for single events, such as what is the probability that it will rain tomorrow. In the Frequentist View, it either rains tomorrow or not. We can ask what the probability is that it rains on the 25th of July in general, by considering the long-run relative frequency of rain on every 25th of July in past, present, and future years. But there is no long-run relative frequency for the 25th of July in 2020.
2.2.1.1 The rules of probability
Although the interpretation of probability is debated, the mathematical rules of calculating probabilities are generally agreed upon. Suppose we have an outcome space \(\mathcal{S} = \{E_1, E_2, E_3, \ldots\}\). That is, the outcome space consists of (abstract) events \(E_1\), \(E_2\), \(E_3\), etc. To refer to any of these, we can use the notation \(E_i\), where \(i\) can equal 1, 2, 3, etc. The rules of probability are then as follows:
- \(0 \leq p(E_i) \leq 1\). The probability of any event \(E_i\) is greater or equal to 0 and smaller than or equal to 1. This rule requires little further explanation. Probabilities are chosen to lie on a scale between 0 and 1.
- \(p(E_1 \text{ or } E_2 \text{ or } E_3 \text{ or } \ldots) = p(\mathcal{S}) = 1\). In words, this means that the probability of at least one event in the outcome space occurring is 1.
- If \(E_i\) and \(E_j\) are mutually exclusive events (if one of them occurs, the other cannot occur), then \(p(E_i \text{ or } E_j) = p(E_i) + p(E_j)\). This is also called the sum rule.
- \(p(\neg E_i) = 1 - p(E_i)\). Here, \(\neg\) means “not”, so the probability of “not \(E_i\)” is 1 minus the probability of \(E_i\) occurring. This is also called the complement rule.
- For any events \(E_i\) and \(E_j\), \(p(E_i \text{ or } E_j) = p(E_i) + p(E_j) - p(E_i \text{ and } E_j)\). This rule holds whether the events are mutually exclusive or not, and can be called the general sum rule.
Now, all these rules seem overkill when we are dealing with a simple coin flip. So let’s consider a slightly more complex situation: betting on the outcome of a roll of a six-sided die. In this betting game, like in roulette, you are allowed to bet on many things, such as the exact number, but also whether the number is odd or even, whether the number is greater than 3, whether the number is greater than 1, etc. All these things are events in the outcome space:
\[\mathcal{S} = \{1, 2, 3, 4, 5, 6, \text{even}, \text{odd}, >3, < 1, \geq 4, 1 \text{ or } 3, \ldots \}\]
The first six events in this outcome space (the numbers 1 to 6) are called elementary events: they are mutually exclusive (a single roll cannot result in both a 1 and a 3), and one of them must occur. So we know that \(p(1) + p(2) + p(3) + p(4) + p(5) + p(6) = 1\). But wait, there are more events in the outcome space, and \(p(\mathcal{S}) = 1\), and these six events are only a small part of the outcome space, so does that imply that they all have probability 0? No! That is because not all events in the outcome space are mutually exclusive. For instance, if the outcome is 5, then the outcome is also odd, and it is also \(>3\), \(\geq 4\), etc. As you might have noticed, the other events are actually themselves sets of the elementary events. For instance, \(\text{odd} = \{1, 3, 5\}\), \(\text{even} = \{2, 4, 6\}\), and \(> 3 = \{4, 5, 6 \}\). Figure 2.3 depicts the relations between these events, as well as the elementary events.
Figure 2.3: A diagram depicting the relations between 9 events in the outcome space of the die betting game
We just really need two more rules and then we’re done. These rules are to compute the probability of a conjunction of events (the probability of both events occurring). To be able to state these rules, we first need to consider the concept of conditional probability. In words, such a probability refers to the probability of one event given that another event occurred. For instance, we can consider the probability of the event “greater than 3” given that the event “odd” occurred (i.e., the probability that the outcome was greater than 3 given that the outcome was an odd number). If we know that the outcome was odd (i.e. 1, 3, or 5), we can rule out all occurrences where the outcome was even (i.e. 2, 4, or 6). To now consider the probability that the outcome was greater than 3, we only need the probability of an outcome greater than 3 within the set of odd numbers. If we are sure that the outcome was odd, we can set \(p(\text{odd}) = 1\). There are three outcomes, each with equal probability, so \(p(1|\text{odd}) = p(3|\text{odd}) = p(5|\text{odd}) = \frac{1}{3}\). In the set of odd outcomes, there is only one number greater than 3, namely 5. That means that the conditional probability \(p(>3|\text{odd}) = p(5|\text{odd}) = \frac{1}{3}\). Conversely, we can also work out the conditional probability \(p(\leq 3|\text{odd}) = p(1|\text{odd}) + p(3|\text{odd}) = \frac{2}{3}\). In a sense, a conditional probability is just looking at the relative occurrence of one event \(E_i\) (e.g., the event “\(>3\)”) within the set of outcomes defined by another event (e.g., the event “odd”).
\[p(E_i|E_j) = \frac{p(E_i \text{ and } E_j) }{p(E_j)}\]
- \(p(E_i \text{ and } E_j) = p(E_i) \times p(E_j | E_i)\). Multiplication rule
- For two independent events \(E_i\) and \(E_j\), \(p(E_i \text{ and } E_j) = p(E_i) \times p(E_j)\)
Kolmogorov, a rather brilliant mathematician, showed that you only need rules 1, 2 and 3; all the other rules follow from the first three. In mathematical terms, rules 1, 2, and 3 are axioms, statements which we assume are true without being able to prove them, while the remaining rules are theorems, statements which follow from the axioms and can be proven to be true.
2.2.1.2 A model of flipping an unbiased coin
Now that we know more about probability, let’s get back to our model for Paul. With a balanced coin (and a not too cunning flipper), the probability of the coin landing heads should equal the probability of the coin landing tails. In mathematical notation, we can state this as
\[p(\text{heads}) = p(\text{tails})\]
Furthermore, as heads and tails are the only two possible outcomes, we know that
\[p(\text{heads} \text{ or } \text{tails}) = 1\] Finally, because heads and tails are two mutually exclusive and equally likely events, we then infer that
\[p(\text{heads}) = p(\text{tails}) = 0.5,\] and given the way Paul bases his decisions on this coin flip, also that \[p(\text{paul left}) = p(\text{paul right}) = 0.5.\]
Interestingly, if Paul made his decision for the left or right box by flipping a coin, it doesn’t really matter whether the team representing the left or right box was chosen randomly, or in some other way. Suppose that Paul’s keeper was very knowledgeable about football, or that he was the real psychic. Furthermore, let’s suppose that he thinks Paul might generally prefer the right box (as the light is particularly nice on that side of the tank, for instance). Then \(p(\text{winner right}) = 1\) and \(p(\text{winner left}) = 0\). Because Paul’s decisions are independent from which team was placed in which box (he’s merely flipping a coin), we know that \(p(\text{paul left} | \text{winner left}) = p(\text{paul left})\), and similarly \(p(\text{paul right} | \text{winner left}) = p(\text{paul right})\). There are two ways in which Paul can make a correct prediction: he opens the right box, and the winning team was in the right box, or he opens the left box and the winning team was in the left box. So \[p(\text{correct}) = p(\text{paul left} \text{ and } \text{winner left}) + p(\text{paul right} \text{ and } \text{winner right})\] Using the multiplication rule, we can write this as \[p(\text{correct}) = p(\text{paul left} | \text{winner left}) \times p(\text{winner left}) + \\ p(\text{paul right} | \text{winner right}) \times p(\text{winner right})\] And from the independence between Paul’s decisions and the assignment of teams to boxes, we can simplify this further as \[p(\text{correct}) = p(\text{paul left}) \times p(\text{winner left}) + p(\text{paul right}) \times p(\text{winner right})\] which, filling in the appropriate values, becomes \[p(\text{correct}) = .5 \times 0 + .5 \times 1 = .5\] Actually, you can fill in any valid probability for \(p(\text{winner left})\) and \(p(\text{winner right})\), and \(p(\text{correct})\) will always be .5! Let’s say, in abstract terms, that \(p(\text{winning left}) = w\). From the complement rule, we know that \(p(\text{winning right}) = 1 - w\). Then \[\begin{aligned} p(\text{correct}) &= p(\text{paul left}) \times w + p(\text{paul right}) \times (1-w) \\ &= .5 \times w + .5 \times (1-w) \\ &= .5 \times w - .5 \times w + .5\\ &= .5 \end{aligned}\] So according to our model, no matter what bias Paul’s keeper might have in placing winning teams in the left or right box, Paul’s accuracy for each prediction would be \(p(\text{correct}) = .5\).
2.2.2 Distributions
A probability distribution, as the name suggests, defines how probability is distributed over all possible values of a variable. You can think of “all probability” as a pie, and the probability distribution as slicing up the pie in (possibly unequal) pieces. Each possible value of a variable is given its own slice, and the size of the slice relative to the overall pie is the probability. Looking at the correctness of a single prediction, the pie is divided into two equal slices: half for \(p(\text{correct})\), and the other half for \(p(\text{incorrect})\). But Paul made more than one prediction (8 in the case of the 2010 FIFA World cup), and what we’re really interested in is Paul’s accuracy in all his predictions: What is the probability that Paul made 8 out of 8 correct predictions if he was merely guessing? Using the rules of probability, we can work out this probability as well.
According to our coin-flipping model, it does not matter which of Paul’s prediction we look at (e.g. whether the first, the second, the last, or any other one). In fact, we could generate the data in the reverse order, or start with the Germany-Australia match and then the Spain-Germany match. Let’s write Paul’s predictions as a variable \(\texttt{pred}_i\), where the index \(i\) can be a value between 1 and 8, corresponding to the first, second, etc., prediction he made. The probability that any prediction is correct is \(p(\texttt{pred}_i = \text{correct}) = .5\), and whether that prediction is correct is independent from whether any earlier (or later) prediction is correct. In fancy terms, this means that the observations \(Y_i\) are independent and identically distributed (IID).
When considering the probability of a sequence of events (e.g. a consecutive run of 8 correct predictions), it can be useful to draw all possible outcomes in the form of a tree. In Figure 2.4, we show such a tree for the first three of Paul’s predictions according to our model in which he was randomly guessing. Starting at the “root node” on the left, the first guess can be either correct or incorrect, and these two outcomes are represented as separate branches. If the first guess was correct, we take the “correct” branch. The next guess can be either correct or incorrect, which splits this branch into two further branches, and so forth.
Figure 2.4: Outcome tree for three random guesses.
For three coin flips, there are 8 unique sequences of outcomes (the tree ends in 8 branches). Because the probability of “heads” and “tails” are identical, and each coin flip is independent of the others, each unique sequence such as “correct, correct, incorrect” has exactly the same probability, namely \(0.5 \times 0.5 \times 0.5 = (0.5)^3 = 0.125\). However, if we are not interested in the probability of a unique sequence of outcomes, but rather the total number of correct guesses, the corresponding probabilities are not equal. For example, there is only one sequence in which the number of correct guesses is 3, but there are three sequences in which the number of correct guesses equals 2. Each of these sequences has the sample probability, so we can just add these up \[p(\text{2 correct and 1 incorrect}) = 3 \times 0.125 = 0.375\] Similarly, the probability \(p(\text{1 correct and 2 incorrect}) = 0.375\), as there are three sequences in which the number of correct guesses equals 1.
Note that we have used a distribution over the outcomes of a single variable (a single prediction) to effectively construct three variables (\(\texttt{pred}_1\), \(\texttt{pred}_2\), and \(\texttt{pred}_3\)) reflecting Paul’s first, second, and third prediction, respectively. We can take the outcomes of each of these three variables and turn this into a new variable reflecting the outcome of all three predictions. This new variable has 8 possible outcomes (unique sequences), each with an equal probability of occurring. Finally, we can then use this sequence variable to construct yet a new variable, the one we are really interested in, reflecting the number of correct predictions. This variable (in the case of three predictions), has four unique outcomes (0, 1, 2, or 3 correct) with unequal probabilities. Perhaps all these variables make your head spin. But a main thing to realize is that from a quite simple model of the Data Generating Process (the outcome of each prediction is an independent coin flip), we can start to say something about how likely Paul’s performance of 8 out of 8 correct predictions really was.
To work out the probability distribution of the number of correct predictions out of 8, we could expand the tree of 2.4, but the tree would become very large. There is a simpler way to count the number of sequences with a particular number of correct predictions in them. The number of sequences of \(n\) predictions where \(k\) predictions are correct can be computed as \[\frac{n!}{k!(n-k)!} ,\] where the exclamation mark refers to the so-called factorial function, where a positive integer is multiplied by all positive integers which are smaller than it. So \[n! = n \times (n-1) \times (n-2) \times (n-3) \times \ldots \times 2 \times 1\] Furthermore, there is the convention that \[0! = 1\]
So we can write \[p(k \text { correct and } n-k \text{ incorrect}) = \frac{n!}{k! \times (n-k)!} (0.5)^n\] For example, we can work out the probability of \(k=8\) correct and \(n-k=0\) incorrect as \[\begin{aligned} p(8 \text { correct and } 0 \text{ incorrect}) &= \frac{8 \times 7 \times ... \times 2 \times 1}{(8 \times 7 \times ... \times 2 \times 1) \times 1} (0.5)^8 \\ &= \frac{1}{1} (0.5)^8 = 0.004 \end{aligned} \] As another example, the probability of \(k=3\) correct and \(n-k=5\) incorrect is \[\begin{aligned} p(8 \text { correct and } 0 \text{ incorrect}) &= \frac{8 \times 7 \times ... \times 2 \times 1}{(3 \times 2 \times 1) \times (5 \times 4 \times 3 \times 2 \times 1)} (0.5)^8 \\ &= \frac{40320}{6 \times 120} \times (0.5)^8 = 56 (0.5)^8 = 0.219 \end{aligned} \] We can follow the same procedure to compute the probability of all other outcomes. The resulting distribution is depicted in Figure 2.5.Figure 2.5: probability distribution over the number of correct predictions out of 8, assuming random guessing.
2.3 Flipping a biased coin: An alternative model
Suppose that Paul did not make his decisions by flipping a mental coin. Perhaps Paul had extensive knowledge of all things football, or perhaps he could see into the future. In that case, we might expect Paul to have a higher rate of correct answers than predicted by our coin flipping model. But perhaps Paul, although an oracle, wasn’t so benevolent to his caretakers, or didn’t want to spoil the match for them. In that case, we might expect the rate of correct answers to be lower than predicted by the coin flipping model. In both cases, we’d expect the probability of a correct answer to be different from .5: \(p(\text{correct}) \neq .5\). But whilst not .5, we don’t otherwise know the value. We call such an unknown value which determines a probability distribution a parameter. We will generally use symbols from the Greek alphabet to denote such parameters. Here, we will use \(\theta\) (pronounced as “thee-ta”). Our alternative to the coin flipping model can now be stated as:
\[p(\texttt{pred}_i = \text{correct}) = \theta\]
Like a variable, a parameter such as \(\theta\) can take different values. It belongs to a model, and its value can not be observed, only inferred. As our parameter reflects a probability, we know that it can never be lower than 0, and never larger than 1. So we know that:
\[0 \leq \theta \leq 1 .\]
Note that the possible values in this range includes \(\theta = 0.5\). Our (unbiased) coin flipping model is actually one of the possible versions (a “special case”) of our new, more general model. Some other ways of saying this are that the coin flipping model is contained within, or nested under, the more general new model. As we will see, nested models play an important role in statistical modelling. In particular, we will often compare how well a special-case or nested model describes the data compared to a more general model. In such model comparisons, we will usually refer to the special-case or restricted model as MODEL R, and the more general model as MODEL G. It is important to realise that these names (like variables) are containers and we can put any models in these, as long as the one we put into MODEL R is a special case of the one we put into MODEL G.
To work out the probability of the number of correct predictions according to this model, we can draw a similar tree as in Figure 2.4, but instead of the probability of each branch being 0.5, we’d use \(\theta\) for any branch that leads to correct, and \(1-\theta\) for any branch leading to incorrect. That means that the probability of a particular sequence, such as correct, incorrect, correct, is not \((0.5)^{3}\), but rather \(\theta \times (1-\theta) \times \theta = \theta^2 \times (1-\theta)\). Apart from this, the logic of constructing the probability distribution of \(k\) out of \(n\) correct predictions is the same, and can be computed as \[\begin{equation} p(k \text { correct and } n-k \text{ incorrect}) = \frac{n!}{k! \times (n-k)!} (\theta)^k \times (1-\theta)^{(n-k)} \tag{2.1} \end{equation}\] This distribution is quite common in statistics, and is called the Binomial distribution. Note that if we fill in \(\theta = 0.5\), then \((1-\theta) = 0.5\) and the resulting distribution is exactly the one we worked out for the unbiased coin-flipping model earlier. So our new, more general model can indeed exactly produce the distribution of the simpler model, and this is what we mean when we say that the simpler model is nested under the more general model.
To work out the probability that Paul made 8 out of 8 correct predictions according this new model, we need to know the value of the parameter \(\theta\). But what should this be? There are infinite possible values that might be reasonable (e.g., \(\theta = .9\), or \(\theta = .947873\)). Luckily, we don’t need to pluck one of these values out of thin air: we can use the data we have to estimate the value of this parameter.
2.4 Estimation
Estimation, in some sense, means an “educated guess”. It is a guess, because we cannot be completely sure that we have picked the true value. It is educated because we don’t just pluck the value from thin air: we use information in the data to guide our guess.
There are different ways in which we can use the information in the data to estimate parameters, such as the method of moments, minimum mean square estimation, and maximum likelihood estimation. Here, we will focus on the latter.
2.4.1 Maximum likelihood estimation
The general idea of maximum likelihood estimation can be summarized as follows: Find that value of a parameter \(\theta\) such that the probability assigned to the data at hand by the model based on \(\theta\) is highest.
Let’s think this through. If we pick any particular value for \(\theta\), we can use the Binomial distribution (Equation (2.1)) to work out the probability that Paul made 8 out of 8 predictions. For instance, if we pick \(\theta = .4\), then \[\begin{aligned} p(\text{8 correct and 0 incorrect}) &= \frac{8!}{8! \times 0!} (0.4)^8 \times (0.6)^0 \\ &= 1 \times (0.4)^8 \times 1 = 0.000655 \end{aligned}\] If we pick \(\theta = .95\), on the other hand, we’d get \[p(\text{8 correct and 0 incorrect}) = 1 \times (0.95)^8 \times 1 = 0.663\] which is obviously higher. If we plot \(p(\text{8 correct} | \theta)\), the probability of 8 correct given or conditional upon a particular value of \(\theta\), for all possible values of \(\theta\), we get the curve shown in Figure 2.6.
Figure 2.6: Probability of Paul’s performance in the 2010 FIFA World Cup for all possible values of \(\theta\) in the biased coin-flipping model
Looking at this plot, is it obvious that the probability of Paul’s observed performance is highest in the model with \(\theta = 1\), thus, our maximum likelihood estimate becomes \(\hat{\theta} = 1\). As can be shown mathematically, the maximum likelihood estimate of \(\theta\) for our model and any data set with \(k\) correct out of \(n\) is always \[\begin{equation} \hat{\theta} = \frac{k}{n} , \tag{2.2} \end{equation}\] i.e. equal to the proportion of correct. Estimating a probability as a proportion seems intuitively reasonable. But how good is it really?
2.4.2 Properties of good estimators
An estimator like specified in Equation (2.2) is an algorithm which takes data as input and produces a parameter estimate as output. Evaluating the quality of the resulting estimates is generally done under the assumption that our model represents the Data Generating Process accurately, i.e. our model is a true representation of the DGP. If our model has unknown parameters, that means that there are values for those parameters such that our model produces data with exactly the same distribution as the DGP. We can call those parameter values the true parameter values. Now, even if we have access to such a true model, estimates of its parameters from a given data set are unlikely to be identical to the true parameters. The main reason is that any actual data set will not cover all of the values that are possible from the Data Generating Process, and/or not in their expected proportions. But the fact is that in practice we have to rely on such limited data sets; we never have access to all the data that could be produced by the Data Generating Process. So we will have to work with estimates that are different from the true parameters. One thing we can do is quantify how much our estimates are likely to deviate from the true parameters. This, in a nutshell, is what statistical estimation theory is all about.
Let’s focus on the estimator of \(\theta\) in Equation (2.2) a bit more. For any fixed sample size \(n\) and a particular true value of \(\theta\), the variability in the estimates will be completely determined by the variability in \(k\), the number correct. The variability in \(k\) directly follows from the Binomial distribution itself. If you look at the distribution depicted in Figure 2.5, which is the distribution of \(k\) for \(\theta = .5\), you can see there are 9 possible values for \(k\), and hence also 9 possible values of \(\frac{k}{n}\), the estimator of \(\theta\). Assuming the true parameter equals \(\theta = .5\), each time we generate a new data set of 8 predictions, it is possible that the estimate of \(\theta\) will equal any value \(\left\{\frac{0}{8}, \frac{1}{8}, \frac{2}{8}, \ldots, \frac{7}{8}, \frac{8}{8}\right\}\), because for each new data set, the value of \(k\) can be any value between 0 and 8. Exactly like the values of \(k\), not each of these estimates will be equally likely. For most of the new data sets, the estimate will equal \(\hat{\theta} = \frac{4}{8}\), the true value of \(\theta\). If the true \(\theta = 1\), then there would be no variability in \(k\). It is simply impossible to make a wrong prediction, and hence the estimate would always equal the true value. In this case, how variable the estimates are depends on the true value of \(\theta\). There is no variability whenever \(\theta = 0\) or \(\theta = 1\), and the variability increases the closer \(\theta\) gets to .5.
Because in this case, the variability in the estimates depends on the true value of \(\theta\), which is unknown and the reason we have to estimate this parameter in the first place, we cannot easily say how far off we might expect our estimate to be from the true parameter. Nevertheless, we can still assess how good our estimator is by considering some important properties of good estimators in general: unbiasedness, consistency, and efficiency.
An unbiased estimator gives, on average, estimates which are equal to the true parameter.
A good estimator should become more precise as we have more data. The larger the number of observations from the Data Generating Process, the closer the resulting estimates should be to the true parameters. A consistent estimator is one which provides less variable estimates if we give it more data.
An efficient estimator is an estimator which provides the least possible variable estimates, meaning it is the most consistent possible. Variability in estimates is unavoidable, as data sets are always limited samples from the Data Generating Process. It can be proven mathematically that there is level of variance of the estimates that no unbiased estimator can go below, or no biased estimator with a given level of bias can go below. An estimator for which the variance in the estimates is equal to this lower bound is called efficient. Such an estimator is, in some sense, the Holy Grail of statistical estimation, especially an unbiased one.
In general, maximum likelihood estimators are consistent and (asymptotically) efficient. They are not always unbiased though, although the bias (the difference between the mean estimate and the true value) decreases when the number of observations increases. Given these desirable properties, maximum likelihood estimators are often the estimators of choice.
2.5 Comparing models: Null-hypothesis significance testing
So, at this point, we have three models of Paul’s accuracy in predictions. The biased coin-flipping model with an unknown parameter \(\theta\). The unbiased coin-flipping, or random guessing, model (which is a special case of the first one, with \(\theta = 0.5\)). And an estimated version of the biased coin-flipping model, with \(\hat{\theta} = 1\) (which is also a special case). Now what?
What we would like to know is whether Paul was randomly guessing, or whether he had some psychic abilities. In other words, whether the unbiased coin-flipping model or the biased coin-flipping model provides a better description of the Data Generating Process. While it is reasonable to define a model as providing a better description of the DGP when the distribution it proposes is a better match to the true DGP distribution, this definition is not usable in practice, as we simply don’t know the true DGP distribution. We have to work with the data at hand, and there are many possible ways in which we can use the data to evaluate whether a particular statistical model provides a better description of the DGP. One principled way is to compare the probability assigned to the observed data by each model. This is usually done by computing what is called the likelihood ratio. Suppose we have two versions of the general biased-coin flipping model, one where we assume that the parameter \(\theta\) has a particular value \(\underline{\theta}\), and one where we assume \(\theta\) takes a different specified value \(\underline{\theta}'\). Note that by placing a line underneath a parameter, we denote that it is a particular value of interest. In this case, we are interested in a single variable, namely the number of correct predictions Paul made, which we will denote by \(Y\), our general symbol for the dependent variable. We can then write the likelihood ratio as: \[\frac{p(Y = k | n, \theta = \underline{\theta})}{p(Y = k | n, \theta = \underline{\theta}')}\] At the top (the numerator), is the probability of \(k\) out of \(n\) correct when the probability of a single prediction correct equals \(\underline{\theta}\). The bottom part (the denominator), is the same probability if the probability of a single correct prediction equals another value \(\underline{\theta}'\). Suppose \(\underline{\theta} = .5\) (as in the random guessing model), and \(\underline{\theta}' = 1\), as in the estimated biased coin-tossing model. The likelihood ratio is then \[\frac{p(Y = 8 | n = 8, \theta = 0.5)}{p(Y = 8 | n = 8, \theta = 1)} = \frac{0.00391}{1} = 0.00391\] What does this mean? Well, if both models assigned the same probability to the observed data, the likelihood ratio would equal one. If the probability according to the model of the numerator is higher, the value of the likelihood ratio would be greater than 1. And if the probability according to the model of the denominator is higher, the value of the likelihood ratio would be smaller than 1. So, as is clear, the model with the estimated value of \(\theta\) assigns a higher probability to the observed data. But that is no wonder! We estimated \(\theta\) by maximum likelihood, meaning that no other value of \(\theta\) could assign a higher probability to the data! If it did, our estimate would simply not be the maximum likelihood estimate. So, if the model in the denominator is the one estimated by maximum likelihood, we know the likelihood ratio could never be larger than 1.
So that’s a little annoying. What seemed like a reasonable way to compare two models that describe a particular data set, now seems pretty useless. We cannot use the general biased coin-flipping model to compute the likelihood ratio, because without choosing a particular value for \(\theta\), the model can not be used to compute the probability of the data. And we can not just use the estimated value of \(\theta\), because then that model would always win the “likelihood competition”. But computing likelihood ratio’s is not, in fact, completely useless. We just need to take into account the fact that the estimated model will always win. What then matters is: by how much?
The null-hypothesis significance test provides an answer to “by how much should the estimated model be better to refute an alternative model?”. The logic is roughly as follows: Suppose the restricted model (MODEL R, e.g. the one where \(\theta = .5\)) is the true model. Then we can use this model to simulate lots of data sets. For each data set, we can estimate \(\theta\) to give us an estimated version of the general model (i.e. MODEL G, the one with \(\theta\) unknown). Then we can use both models to compute a value of the likelihood ratio. For each data set, the likelihood ratio may take a different value. What we end up with is thus a distribution of values of the likelihood ratio, produced by MODEL R. We will know that this likelihood ratio is always below 1, but by inspecting this distribution, we will roughly know what the usual values are, in the case where MODEL R is true. We can then try to find a range of values which are relatively unusual, given that MODEL R is true. If the value of the likelihood ratio we found for the real data is within this range, we might reason that this value is “unusual enough” to reject MODEL R, and accept that MODEL G provides a better description.
So let’s do this. I used MODEL R (the one with \(\theta = .5\)) to simulate 100,000 data sets in which Paul made 8 predictions. For each of these, I estimated MODEL G, and then computed the likelihood ratio for that dataset, comparing MODEL R to the estimated MODEL G: \[\frac{p(Y = k | n = 8, \theta = 0.5)}{p(Y = k | n = 8, \theta = \frac{k}{8})}\] Note that \(k\) is the main thing that varies from simulated dataset to simulated dataset, and that for \(\theta\) in the model of the denominator, I have filled in the maximum likelihood estimate \(\frac{k}{8}\), which also varies over the simulations. I then determined the proportion (out of all 100,000) simulations of each value of the likelihood ratio. You can see the result in Figure 2.7.
Figure 2.7: Likelihood ratio values for 100,000 simulated data sets from MODEL R with \(\theta = .5\)
A first thing to notice is that there are only 5 unique values of the likelihood ratio in all 100,000 simulations. This is not a strange coincidence. While there are 9 possible values of \(k\) for datasets with \(n=8\), some of these will provide exactly the same likelihood ratio. For example, the likelihood ratio is identical for \(k=3\) and \(k=5\): \[\frac{p(Y = 3 | n = 8, \theta = 0.5)}{p(Y = 3 | n = 8, \theta = \frac{3}{8})} = \frac{p(Y = 5 | n = 8, \theta = 0.5)}{p(Y = 5 | n = 8, \theta = \frac{5}{8})} = 0.777\] Similarly, the value of the likelihood ratio is identical for \(k=2\) and \(k=6\), for \(k=1\) and \(k=7\), and for \(k=0\) and \(k=8\). With that out of the way, let’s look at how often each of these 5 possible values occurred. As MODEL R was the true model (we used it as the Data Generating Process for our simulations), you might expect that a likelihood ratio of 1 would be the most frequent value, as that would imply that MODEL R and (estimated) MODEL G provide an equally good description of a data set. But while this value occurs relatively frequently (27.45%), the most common value is actually 0.777 (43.694%). Only the value of 0.00391 is rather unlikely (0.735%). In all our simulations, less than 1% had a value of the likelihood ratio as low as the one we found for the real data. Thus, if MODEL R is true, we would not expect an estimated MODEL G to perform as well very often. But is that reasonable grounds to conclude MODEL G provides a better description than the random-guessing MODEL R?
Before we go into this, let me point out that I used the idea of simulating data sets mainly for educational purposes. Although simulation is useful, it is imprecise. Even if we simulate 100,000 data sets, this is still a limited number, and hence any results will differ (even if only slightly) when we simulate another 100,000 data sets. In this case, it is actually quite straightforward to avoid simulation completely. Using the Binomial distribution, it is – with a little thinking – quite easy to work out the distribution of the likelihood ratio comparing MODEL R to estimated versions of MODEL G. Recall that for \(n=8\), there are 9 possible values of \(k\). If MODEL R is true, we know the probability of each of these values from the Binomial distribution. Moreover, each of these values will lead to a different estimate of \(\theta\) in MODEL G, which in turn, paired with the corresponding value of \(k\), each provide a value of the likelihood ratio. Let’s collect all these things in a table:
| \(k\) | \(p(k \mid \theta = .5)\) | \(\hat{\theta}\) | \(p(k \mid \theta = \hat{\theta})\) | likelihood ratio |
|---|---|---|---|---|
| 0 | 0.00391 | 0.000 | 1.000 | 0.00391 |
| 1 | 0.03125 | 0.125 | 0.393 | 0.07958 |
| 2 | 0.10938 | 0.250 | 0.311 | 0.35117 |
| 3 | 0.21875 | 0.375 | 0.282 | 0.77672 |
| 4 | 0.27344 | 0.500 | 0.273 | 1.00000 |
| 5 | 0.21875 | 0.625 | 0.282 | 0.77672 |
| 6 | 0.10938 | 0.750 | 0.311 | 0.35117 |
| 7 | 0.03125 | 0.875 | 0.393 | 0.07958 |
| 8 | 0.00391 | 1.000 | 1.000 | 0.00391 |
Figure 2.8: The true distibution of likelihood ratio’s comparing MODEL R with estimated MODEL G, when the true model is MODEL R.
When you compare this plot to Figure 2.7, you see there are indeed very alike. So we don’t need to simulate data to determine what values of the likelihood ratio we might see – and how often – if MODEL R is true. MODEL R allows us to easily compute the probability of each possible number of correct guesses, \(k\). This number, in turn, determines everything else of interest: the estimates of \(\theta\) for MODEL G, the probability of the data according to (the estimated) MODEL G, and the likelihood ratio between MODEL R and (the estimated) MODEL G. When possible, it is better to work out the distribution like we did here, instead of relying on simulation. Simulation is inherently noisy, even with 100,000 samples.
That’s all well and good, you might object, but you have done all this by assuming that MODEL R is true. But we don’t know whether MODEL R is true, we don’t know that Paul was randomly guessing. In fact, the question whether he was actually psychic (and not randomly guessing) is what brought us to this point in the first place! That is indeed very true. The issue is that there are many ways in which MODEL R can be false and MODEL G true. In fact, there are an infinite number of values for \(\theta\) which aren’t equal to 0.5. Each of these implies a different distribution of the likelihood ratio where we compare MODEL R (with \(\theta = .5\)) to the estimated MODEL G (with \(\hat{\theta} = \frac{k}{n}\)). Some examples are given in Figure 2.9. If we assume that MODEL R is false, then any of these distributions would be the true distribution of the likelihood ratio. But without knowing the exact value of \(\theta\), we simply don’t know which one.
Figure 2.9: The true distibution of likelihood ratio’s comparing MODEL R with estimated MODEL G, when the true model is MODEL G with different values of \(\theta\).
2.5.1 Decisions and types of error
Let’s relocate ourselves. We started by defining a model in which Paul was randomly guessing (MODEL R). We then defined another model in which Paul could be (somewhat) psychic, but as we don’t know how psychic and whether Paul would want to make correct predictions or incorrect predictions. In this model, Paul’s probability of making a correct prediction could be anything. Because it is so general, MODEL G can effectively predict anything. We can use the data to estimate MODEL G. But doing that, it makes MODEL G a bit like an annoying friend, who always says “I knew that was going to happen” after it happened, but never before. Because MODEL G is so fickle, our procedure focuses almost exclusively on MODEL R, the version of MODEL G (remember, MODEL R is a special case of MODEL G) which is much more strident, and does tell us how likely things are to happen before they happen.
In the null hypothesis significance test, the hypothesis that MODEL R is true is called the null hypothesis, or \(H_0\), in the conventional notation: \[H_0: \text{MODEL R is true}\] This hypothesis itself may be either true or false. If \(H_0\) is true, then MODEL R is true. If \(H_0\) is false, then the statement “MODEL R is true” is false, so MODEL R is false. These are the two possibilities that we are faced with, but we don’t know which of these is actually the case.3 Based on data, we can decide to accept \(H_0\) as a true statement, or reject \(H_0\). But these decisions can be correct, or incorrect. Combining the actual state of the world with our decisions, we have the following four possibilities:
| accept \(H_0\) | reject \(H_0\) | |
|---|---|---|
| \(H_0\) is true | correct | error (Type 1) |
| \(H_0\) is false | error (Type 2) | correct |
If \(H_0\) is actually true, and we accept \(H_0\), we can rejoice, as we made a correct decision. Similarly, if \(H_0\) is actually not true, and we reject \(H_0\), we can also rejoice, as this is another correct decision. If, on the other hand, \(H_0\) is true, but we reject \(H_0\), we made a wrong decision. This is called a Type 1 error. A type 2 error refers to making the other wrong decision, namely if we accept \(H_0\), but \(H_0\) is in fact false.
Null hypothesis significance testing is a procedure to make a decision based on data such that we can limit the chances of making one of these errors, namely the Type 1 error.
2.5.2 Significance and power
In null hypothesis significance testing, we focus on the probability of making a Type 1 error, which is usually denoted as \(\alpha\): \[\begin{equation} \alpha = p(\text{reject } H_0| H_0 \text{ is true}) \tag{2.3} \end{equation}\] It is also referred to as the significance level. If \(H_0\) is true, then we can define a decision procedure to either accept or reject \(H_0\), such that we know the probability of a Type 1 error, and moreover, we can set this probability to a desired value.
Let’s consider Figure 2.8 again. This is the theoretical distribution of the likelihood ratio values when MODEL R is true, i.e., when \(H_0\) is true. Large values of the likelihood ratio indicate that MODEL G does not provide a much better fit to the data than MODEL R, so it makes sense that such large values should not persuade us to reject MODEL R. Values close to 0, on the other hand, indicate that MODEL G does provide a substantially better fit to the data than MODEL R. Hence, it makes sense to decide to reject \(H_0\) if the likelihood ratio is “close enough” to 0. Clearly, such low values can occur even if \(H_0\) is true (as Figure 2.8 attests). But they are unlikely to do so. If \(H_0\) is false, such low values become more likely (see Figure 2.9).
The idea is now to pick a cutoff value for the likelihood ratio such that if we find a value equal to or smaller than it, we reject the null hypothesis. We choose this cutoff value, called the critical value, by considering the probability of the values, assuming MODEL R is true (as this is the only model that can provide us with a proper distribution). More precisely, we choose the critical value such that the probability of making a Type 1 error does not exceed a chosen value, called the significance level, which is usually set to \(\alpha = .05\). That means that, if \(H_0\) is true, we are allowing at most 5% of our tests to result in a Type 1 error. So how do we pick this critical value? Let’s again consider the theoretical distribution of the likelihood ratio we worked out and depicted in Figure 2.8. As it is difficult to see the precise probabilities in this figure, let’s first create another table like the one we did before, but now focussing specifically on the values of the likelihood ratio. Table 2.3 doesn’t really contain any more information than Table 2.2. We have simply added up some of the numbers in that table. A new concept though is that of a cumulative probability, by which we mean the probability of a given value or any lower value. Here, we focus on the cumulative probability for the likelihood ratio, \(p(\text{likelihood ratio} \leq \text{value})\). Such cumulative probabilities are interesting here, because we want to find a cutoff value, and then limit the probability of getting any values lower than it to the significance level \(\alpha\).
| value | \(p(\text{likelihood ratio} = \text{value})\) | \(p(\text{likelihood ratio} \leq \text{value})\) |
|---|---|---|
| 0.00391 | 0.00781 | 0.00781 |
| 0.07958 | 0.06250 | 0.07031 |
| 0.35117 | 0.21875 | 0.28906 |
| 0.77672 | 0.43750 | 0.72656 |
| 1.00000 | 0.27344 | 1.00000 |
Let’s look at the cumulative probabilities (simply computed by adding, on each row of the table, the value of \(p(\text{likelihood ratio} = \text{value})\) on that row, and all rows above it). How should we place our critical value to ensure that \(\alpha \leq .05\)? If we picked the value 0.07958, and rejected the null hypothesis if we obtained a value equal to or lower than that, then the probability of a Type I error would be 0.07031. Thus, if we don’t want that probability to be higher than .05, then we can’t pick that value. If, on the other hand, we pick the value 0.00391, then the probability of a Type I error would be 0.007813, which is lower than \(\alpha = .05\). As we should not go higher than our desired value of \(\alpha\), that would be the appropriate critical value.4 Indeed, we could place the critical value somewhere between 0.003906 and 0.07958, as I have done in Figure 2.10 to make the plot easier to read. As, with \(n=8\), there are no possible values of the likelihood ratio between 0.003906 and 0.07958 anyway, the precise placement of the critical value does not really matter.
Figure 2.10: Critical values (dotted lines) and the true distibution of likelihood ratios comparing MODEL R with estimated MODEL G, when the true model is MODEL R (left) and the true model is one particular version of MODEL G (right).
The plot on the left of Figure 2.10 shows the situation considered by the null hypothesis significance test, namely the situation in which MODEL R is true. If MODEL R is false, then \(\theta\) can, in principle, take any value \(\theta \neq 0.5\). If \(\theta\) does not equal 0.5, the probability \(p(\text{likelihood ratio} \leq \text{critical value})\) will be higher than when \(\theta = 0.5\). As an example, the right side of Figure 2.10 shows that \[p(\text{likelihood ratio} \leq \text{critical value} | \theta = 0.9) = 0.43\] This probability of obtaining a value equal to or lower than the critical value, given that \(H_0\) is false, is also called the power of a test:
\[\begin{equation} \text{power} = p(\text{test value} \leq \text{critical value} | H_0 \text{ is false} ) \tag{2.4} \end{equation}\] Note that I’m using “test value” rather than likelihood ratio, because there will be times when we use a different test statistic than the likelihood ratio, and I want the definition of power here to cover those situations too. Furthermore, the complementary probability, \(p(\text{value} > \text{critical value} | H_0 \text{ is false})\), is the probability of a Type 2 error. Now, while power is a very important concept in hypothesis testing, it is also elusive. If you look at Figure 2.9, you can see that the power is different for different values of \(\theta\).
Power is an important concept because usually, it is less interesting if the null hypothesis is true than if it is false. For instance, it is less interesting if Paul was merely guessing than if he was psychic. So usually, we are more interested in rejecting the null hypothesis than in accepting it. Disappointingly, in this case, the power is pretty low even when \(\theta = .9\), and it is even lower for values of \(\theta\) closer to 0.5. We can increase the power by increasing \(\alpha\). You can visualize this in Figure 2.10 as moving the critical value to the right, for instance to the right of the second possible value of the likelihood ratio. If \(\theta = .9\), that would increase the power to 0.813. But conversely, the probability of a Type 1 error would now be 0.07. Generally speaking, we don’t want the probability of a Type 1 error so high. A better way of increasing the power of a test is to collect more data; e.g., by letting Paul make more predictions than 8.
The tricky thing about the power of a test is that it depends on the unknown parameter \(\theta\), and can never really be known. We can calculate the power of a test for various values of \(\theta\), but in a sense, the choice of such values is arbitrary if we don’t know the true value of \(\theta\). Of course, using our data, we could estimate \(\theta\), and then calculate what some have called the “observed power” of a test. In this example, \(\hat{\theta} = \frac{8}{8} = 1\), and the “observed power” is 1. But, as we know, the estimate of \(\theta\) is not identical to the true value of \(\theta\), and hence the estimated power is unlikely to be equal to the true power, unless we have a lot of data, but then the power would be reasonably large in the first place. As such, “observed power” is rather useless. Perhaps the most useful way (at least in my opinion) to consider power is to determine the value of \(\theta\) that would provide a reasonable level of power. Conventionally, a power of \(p(\text{test value} \leq \text{critical value} | H_0 \text{ is false} ) = 0.8\) is considered reasonable. By plotting the power for different values of \(\theta\), as done in Figure 2.11, we can then determine the values of \(\theta\) which would obtain this level of power. Such a plot is also called a power-curve. As you can see, values of \(\theta\) close to 0 and 1 provide a high power. To reach a power of at least 0.8, it would need to be the case that \(\theta \leq 0.028\) or \(\theta \geq 0.972\). Thus, Paul would have to be rather good at giving correct predictions (or very good at giving incorrect predictions), to make it reasonably likely that we would reject the null hypothesis. If you consider \(\theta \leq 0.028\) or \(\theta \geq 0.972\) too extreme to be likely, then it would be a good idea to get more data in order to make the required value of \(\theta\) more reasonable.
Figure 2.11: A power-curve, plotting the power of the test for different values of \(\theta\). The broken line indicates a power of 0.8, and the dotted lines indicate the values of \(\theta\) which obtain this power.
2.5.3 Testing whether Paul was guessing
Finally then, let’s actually test the null hypothesis that Paul was guessing. When just considering his performance in the 2010 FIFA World cup, Paul made \(n=8\) predictions and \(k=8\) of these were correct. This gives a likelihood ratio of MODEL R (\(\theta = .5\)) over estimated MODEL G (\(\hat{\theta} = 1\)) of 0.00391. Using a significance level of \(\alpha = .05\), the critical value is set to 0.00391, and as the likelihood ratio is equal to or smaller than this value, we reject \(H_0: \theta = .5\), and conclude that it is rather unlikely that Paul was merely guessing. In fact, \(p(\text{likelihood ratio} \leq 0.00391 | \theta = .5) = 0.00781\). This latter probability, the probability of a test value equal to more extreme than the test value calculated for the data, is generally also called the p-value. If the p-value is smaller than the required significance level, the test result is called significant, and we reject \(H_0\). What “more extreme” means can vary, depending on how the test is performed.
Now, in the preceding discussion, we have completely ignored Paul’s performance in the UEFA Euro 2008 cup. If we can assume that Paul’s psychic abilities did not change between the UEFA Euro 2008 and the 2010 FIFA World cup, it makes sense to pool both data sets to get a more reliable and more powerful test. As the logic is entirely the same as before, we will go through this quickly. Pooling both datasets, we now have \(n=14\) predictions, of which \(k= 12\) were correct. This provides a likelihood ratio of \[\text{likelihood ratio} = \frac{p(k=12|n=14, \theta = .5)}{p(k=12|n=14, \hat{\theta} = \frac{12}{14})} = 0.019\]
For \(\alpha = .05\), the critical value is 0.019, so again, we can reject \(H_0: \theta = .5\). In fact, the probability of obtaining a likelihood ratio of 0.019 or smaller if \(H_0\) is true, the p-value, is .0129.
2.6 Hypothesis testing directly with the Binomial distribution
In the preceding, we have focused on the likelihood ratio as the test statistic for our hypothesis tests. The likelihood ratio is a very general measure to compare how well two models describe the data. And it clearly shows how hypothesis testing can be seen as a form of model comparison. That said, the likelihood ratio can also be a bit cumbersome to work with, and deriving the distribution of the likelihood ratio under the null hypothesis is not always straightforward. As we will see later, we can often use a different measure in place of the likelihood ratio, which will provide testing procedures that are equivalent to it.
As we saw when we worked out the theoretical distribution of the likelihood ratio (Table 2.2), there is a direct relation between the number of correct guesses and the value of the likelihood ratio. In a way, you can think of the likelihood ratio as a transformation of the number of correct guesses into a new measure (the likelihood ratio). For example, \(k=8\) out of \(n=8\) correct guesses becomes a likelihood ratio of 0.00391, and \(7\) out of \(8\) correct guesses becomes a likelihood ratio of 0.07958. Similarly, \(k=0\) out of \(n=8\) correct guesses becomes a likelihood ratio of 0.00391, and \(1\) out of \(8\) correct guesses becomes a likelihood ratio of 0.07958. So different values of \(k\) may provide the same likelihood ratio value (in mathematical terms, this is also called a many-to-one mapping). This is similar to outcomes 1, 3, and 5 of a die roll all mapping onto “odd number”.
Because both the value and the probability of likelihood ratio values depend solely on the number of correct guesses, the number of correct guesses contains all the information about the likelihood ratio. Because of this, we can define our hypothesis tests directly in terms of correct guesses, without losing any information. For instance, when we considered the pooled data from the UEFA Euro 2008 cup and the 2010 FIFA World cup, we determined that any likelihood ratio equal to or smaller than 0.00756 would lead to a rejection of the null hypothesis. There are three possible values of the likelihood ratio in this critical region (values between 0 and 0.00756), and these are associated with \(k=0,1,2,12,13,\text{ or } 14\). Thus, we can equivalently define the critical region in terms of the number of correct guesses: \(k \leq 2\) and \(k \geq 12\). Figure 2.12 depicts the distribution of \(k\) under \(H_0\) and the critical region for \(\alpha=.05\).
Figure 2.12: Distribution of the number of correct predictions (\(k\)) out of \(n=14\) under MODEL R (\(\theta = .5\)), and the critical regions for \(\alpha = .05\).
Note that both this new way of testing \(H_0\), as well as the likelihood ratio test we performed earlier, base their decisions on Paul’s number of correct guesses (i.e. \(Y = 12\)). This new way checks directly whether the value of \(Y\) is in the critical region, while the likelihood ratio test first transforms \(Y\) into a likelihood ratio, and then checks whether this value is in the critical region. Both ways of testing provide exactly the same decisions. But testing \(Y\) directly is somewhat easier, as we don’t have to compute anything else. In addition, using \(Y\) directly also makes it more straightforward to perform a one-sided hypothesis test.
Up to now, we have compared a model with \(\theta = .5\) to a model that merely assumed \(0 \leq \theta \leq 1\). The latter model can not only account for Paul making very accurate predictions, but also for Paul making very inaccurate predictions. But perhaps it is more reasonable to expect that if Paul was indeed psychic, that he would make correct predictions, rather than deceiving his keeper by making inaccurate predictions. In other words, if Paul was psychic, we would expect the probability of him making a correct prediction to be larger than if he were just guessing, so \(\theta > .5\). We can still test this model against the null hypothesis of random guessing, but now small numbers of correct guesses should not move us to reject the null hypothesis, as such small numbers would be even less likely if a model with \(\theta > .5\) were true. If we’d use the right critical region of Figure 2.12, the actual significance level would be only \(\alpha = 0.006\) (the probability \(p(k \geq 12 | \theta = .5)\)). If we’d like a significance level of \(\alpha = .05\), we can actually move the critical value to 11, as \(p(k \geq 11 | \theta = .5) = 0.029\), which is still below the desired \(\alpha = .05\), but it is as close as we can get here. The resulting right-sided test of the hypothesis \(H_0: \theta = .5\) versus the alternative that \(\theta > .5\) is depicted in Figure 2.13. The result of this test, with \(Y = 12\), is again to reject \(H_0\).
Figure 2.13: Distribution of the number of correct predictions (\(k\)) out of \(n=14\) under MODEL R (\(\theta = .5\)), and the critical region for a one-sided test and \(\alpha = .05\).
It is possible to formulate this one-sided test in terms of a likelihood ratio test as well, but that wouldn’t necessarily make things clearer, and I think this chapter is long enough already.
2.7 Summary
Statistical models define a probability distribution for the Data Generating Process. To test a particular hypothesis about an aspect of the DGP, such as that the probability of a correct prediction by Paul equals .5, we can define two alternative models, one which assumes the DGP has that characteristic, and one which doesn’t. When it is difficult to decide upon a reasonable alternative value for the hypothesised characteristic of the DGP, the model can leave this value unspecified as a parameter. Generally, apart from the value of the parameter(s), the models are identical in other respects. In that case, the model where we assume we know the value of the parameter(s) is a special case of the more general model where we leave the parameter(s) unspecified. The specified model (e.g., one in which the probability of a correct prediction is \(\theta = .5\)) is then said to be nested within the more general model (e.g., the one in which \(\theta\) can take any value between 0 and 1). We refer to the more general model as MODEL G (the “general” model), and the specified model as MODEL R (the “restricted” model, in which we restrict the value of a parameter to have a specified value).
Unknown parameters of statistical models can be estimated from the data. Maximum likelihood estimation is a widely used and useful method to estimate parameters of statistical models. It estimates parameters by finding the value which maximises the probability of the observed data according to the model. Maximum likelihood estimators are consistent and efficient, although they can be biased.
When comparing statistical models, we want to know how good each is in describing the data. A useful and general measure for this is the likelihood ratio. However, when comparing an estimated model to a model where we restrict the value of the parameter(s) to take a particular value, we know the likelihood ratio will never show the estimated model is worse than the restricted model, as we estimated the model to maximise the likelihood. The idea of null hypothesis significance testing is to consider how the parameter estimates and the likelihood ratio values are distributed if the null hypothesis (the restricted model) is true. The procedure relies on a critical value such that the null hypothesis is rejected if the likelihood ratio is equal to or more extreme than the critical value. the critical value is chosen such that the probability of rejecting the null hypothesis when it is true (a Type 1 error) does not exceed a particular value, called the significance level (\(\alpha\)). The power of a test, the probability of rejecting the null hypothesis when it is false, is also an important concept, but in practice, it is difficult to determine, as it requires knowing the true value of the parameter(s) of the general model.
2.8 Epilogue
Was Paul really psychic? Quite likely not. Paul’s accuracy is quite unlikely if he were randomly guessing, and we have rejected this null hypothesis. That doesn’t mean that the null hypothesis is definitely not true; the null hypothesis significance test merely limits the probability of a wrong rejection to a maximum of e.g. \(\alpha = .05\). In statistics, we can never really be sure of anything. But we shouldn’t use this argument to allow us to conclude whatever we want, because then it becomes rather pointless to test a hypothesis in the first place. So we should really conclude that Paul’s performance was higher than expected if he were guessing. But there are various ways to explain his performance which don’t involve him being psychic. For instance, Germany was a team in a rather disproportionate number of the matches for which Paul provided predictions, and in many of these, he opened the box with the German flag on it first. Perhaps Paul preferred the German flag over most other flags? Germany was also a strong team in both the UEFA Euro 2008 and the 2010 FIFA World cup. These factors could easily combine to allow Paul a large number of correct predictions. You can probably think of other confounds to explain his performance as well.
Paul was not the only animal making predictions about sports matches. Mani the parakeet, Nelly the elephant, Flopsy the kangaroo, Madame Shiva the guinea pig, Big Head the sea turtle, Shaheen the camel, and Achilles the cat, are some other ones with more or less success. And there are probably many more who no one has heard about. If you think of all these animals making predictions as repetitions of a larger experiment (e.g. testing whether animals in general are psychic), it does not seem surprising that in some of these, an animal will make a large number of correct predictions.
But then again, Paul was not just any animal… He was an octopus…with nine brains!
Perhaps it is a little confusing to first talk about models being true, and then about hypotheses stating that these models are true. As it is conventional to talk about the null hypothesis (\(H_0\)) in the context of significance testing, it is important to know what this concept implies though, hence that’s why I’m using it here also.↩︎
Of course, another way to ensure that we never go above \(\alpha\) is to set the critical value to 0. But that would mean we never reject \(H_0\), which makes the test pointless.↩︎